離心機(jī)法校準(zhǔn)加速度計(jì)不確定度的統(tǒng)計(jì)模擬算法
離心機(jī)法校準(zhǔn)加速度計(jì)不確定度的統(tǒng)計(jì)模擬算法
喬仁曉1孟曉風(fēng)2李皎1戴冬冰1
(1.天獅學(xué)院自動(dòng)化學(xué)院,天津301700;2.北京航空航天大學(xué)儀器光電學(xué)院,北京100191)
摘要:加速度計(jì)精密離心機(jī)法校準(zhǔn)的復(fù)雜性,使誤差源的不確定度傳播系數(shù)不滿足顯式解析、可導(dǎo)和近似線性的條件,因而無法應(yīng)用常規(guī)的微積分方法求解。統(tǒng)計(jì)模擬方法是復(fù)雜測(cè)量不確定度計(jì)算的有效方法。通過模擬產(chǎn)生轉(zhuǎn)速和半徑隨機(jī)矢量的多次實(shí)現(xiàn)值,經(jīng)數(shù)據(jù)變換和最小二乘擬合得到加速度計(jì)方程系數(shù)的樣本空間,最后用統(tǒng)計(jì)方法求得系數(shù)的不確定度,與離心機(jī)實(shí)驗(yàn)法校準(zhǔn)結(jié)果比較,具有較高的一致性,證明了統(tǒng)計(jì)模擬方法的有效性。
關(guān)鍵詞:離心機(jī);加速度計(jì);校準(zhǔn);不確定度;統(tǒng)計(jì);模擬
中圖分類號(hào):TB9文獻(xiàn)標(biāo)識(shí)碼:A國(guó)家標(biāo)準(zhǔn)學(xué)科分類代碼:120.1470
1·引言
高精度慣導(dǎo)加速度計(jì)的靜態(tài)特性校準(zhǔn)主要通過精密離心機(jī)實(shí)現(xiàn),離心機(jī)輸出加速度的精度是決定加速度計(jì)靜態(tài)方程系數(shù)估計(jì)精度的根本因素。離心機(jī)輸出加速度量值大小由轉(zhuǎn)速和工作半徑確定,輸出精度也主要取決于轉(zhuǎn)速與工作半徑的精度,并受失準(zhǔn)角等因素影響[1]。隨著航空航天、國(guó)防軍工等尖端領(lǐng)域?qū)€加速度計(jì)精度要求的不斷提高,離心機(jī)的輸出精度也必須進(jìn)一步提高,從而要求工作半徑和轉(zhuǎn)速的測(cè)量、控制精度必須進(jìn)一步提高。由于無法通過求導(dǎo)得到誤差源不確定度傳播系數(shù)的顯式解析表達(dá)式,使得基于微積分的常規(guī)誤差傳遞分析方法難以實(shí)現(xiàn)。近年來,蒙特卡羅統(tǒng)計(jì)方法被應(yīng)用于復(fù)雜測(cè)量的不確定度估計(jì),并得到國(guó)際計(jì)量局(BIPM)等國(guó)際組織的認(rèn)可和推行[2-3]。本文通過模擬直接測(cè)量物理量的量值和數(shù)據(jù)變換,得到多維、非線性間接測(cè)量結(jié)果的樣本,用統(tǒng)計(jì)的方法得到最終測(cè)量結(jié)果不確定度。
2·不確定度統(tǒng)計(jì)模擬基本原理
統(tǒng)計(jì)模擬方法又稱為蒙特卡羅方法(MonteCarlo method),是一種以概率統(tǒng)計(jì)為基礎(chǔ)的數(shù)值計(jì)算方法。它能比較逼真地描述和模擬事物的特征和物理過程。特別是對(duì)于那些由于計(jì)算過于復(fù)雜而難以得到解析解或者根本沒有解析解的問題,如復(fù)雜的隨機(jī)問題和非線性問題,蒙特卡羅方法是一種有效的求出數(shù)值解的方法。在測(cè)試計(jì)量領(lǐng)域,由于測(cè)量過程中往往存在許多隨機(jī)因素,蒙特卡羅方法特別適合模擬測(cè)量過程中的各種誤差因素的影響,近幾年來被廣泛應(yīng)用于測(cè)量不確定度的評(píng)定[4-8]。不確定度統(tǒng)計(jì)模擬分析過程包括源數(shù)據(jù)仿真、數(shù)據(jù)變換、統(tǒng)計(jì)綜合3部分。源數(shù)據(jù)仿真是指根據(jù)n個(gè)不確定度來源的概率分布信息模擬生成對(duì)應(yīng)的n維隨機(jī)變量的實(shí)現(xiàn)值;數(shù)據(jù)變換是根據(jù)測(cè)量的實(shí)際物理過程和數(shù)學(xué)處理算法對(duì)n維隨機(jī)變量進(jìn)行運(yùn)算變換,得到間接測(cè)量結(jié)果。這兩個(gè)過程重復(fù)多次,得到間接測(cè)量結(jié)果的一個(gè)樣本空間;統(tǒng)計(jì)綜合就是對(duì)間接測(cè)量結(jié)果樣本空間的樣本進(jìn)行統(tǒng)計(jì)分析得到最終的數(shù)據(jù)結(jié)果[9]。具體過程如圖1所示。
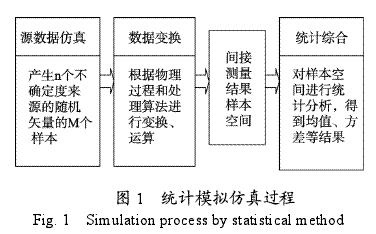
3·加速度計(jì)系數(shù)不確定度統(tǒng)計(jì)模擬
3.1加速度計(jì)離心機(jī)法校準(zhǔn)建模
線加速度計(jì)的三次多項(xiàng)式靜態(tài)輸入輸出特性模型為:
![]()
式中:a為沿離心機(jī)IA軸(輸入軸)方向的輸入加速度,e為加速度計(jì)輸出值;ki,i=0,1,2,3為靜態(tài)特性方程的各次項(xiàng)系數(shù)。
作為標(biāo)準(zhǔn)裝置的精密離心機(jī),在忽略其他誤差因素的情況下,輸出加速度主要取決于離心機(jī)工作半徑R和轉(zhuǎn)速ω,關(guān)系式為:

![]()
3)統(tǒng)計(jì)綜合
根據(jù)樣本空間數(shù)據(jù),擬合得到隨機(jī)變量K的概率分布函數(shù)向量


計(jì)算加速度計(jì)各次項(xiàng)系數(shù)估計(jì)值ki及其標(biāo)準(zhǔn)測(cè)量不確定度u(ki)。其中積分區(qū)間為整個(gè)樣本空間Ω。
4·統(tǒng)計(jì)模擬分析實(shí)例
分別用精密離心機(jī)實(shí)驗(yàn)法和統(tǒng)計(jì)模擬數(shù)值方法對(duì)某加速度計(jì)靜態(tài)特性方程系數(shù)進(jìn)行不確定度分析。表1為用精密離心機(jī)LXJ-40實(shí)驗(yàn)校準(zhǔn)的結(jié)果,表2為用統(tǒng)計(jì)模擬方法10 000次仿真值統(tǒng)計(jì)分析的結(jié)果[10]。由表中數(shù)據(jù)可以看出,兩種方法的校準(zhǔn)結(jié)果具有較好的一致性。特別是作為主成分的一次項(xiàng)系數(shù)估計(jì)值及其不確定度估計(jì)值都有很高的準(zhǔn)確度。偏值系數(shù)不確定度uk0值有較明顯差別但量級(jí)相同,這是由于在統(tǒng)計(jì)模擬方法中只對(duì)主體變量ω和R的隨機(jī)誤差進(jìn)行了仿真而忽略了一些次要誤差因素,如加速度計(jì)輸出值測(cè)量誤差ue等因素的影響,而這些因素在實(shí)際離心機(jī)試驗(yàn)中都產(chǎn)生影響。
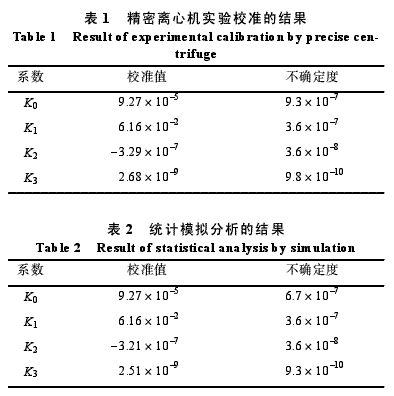
另外,無論是統(tǒng)計(jì)仿真,還是實(shí)際離心機(jī)試驗(yàn),加速度點(diǎn)數(shù)的選擇和起始點(diǎn)的位置都會(huì)對(duì)最終結(jié)果產(chǎn)生微小的影響。
5·結(jié)論
傳統(tǒng)的不確定度評(píng)定方法在某些復(fù)雜間接測(cè)量中遇到困難。現(xiàn)代計(jì)算機(jī)技術(shù)的飛速發(fā)展使計(jì)算機(jī)容量和運(yùn)算速度大大提高,特別是虛擬化技術(shù)、網(wǎng)格計(jì)算、云計(jì)算技術(shù)的發(fā)展和應(yīng)用,使得大樣本容量的復(fù)雜運(yùn)算的仿真變得容易實(shí)現(xiàn)[11-15],為近幾年來逐漸發(fā)展的以大規(guī)模運(yùn)算為基礎(chǔ)的統(tǒng)計(jì)模擬方法提供了技術(shù)手段。在擁有足夠概率分布信息的情況下,統(tǒng)計(jì)模擬方法既能同時(shí)對(duì)絕對(duì)誤差和相對(duì)誤差的影響進(jìn)行合乎實(shí)際的仿真,并避開復(fù)雜的有時(shí)甚至難以實(shí)現(xiàn)的不確定度合成計(jì)算問題,得到穩(wěn)定、可信的測(cè)量不確定度結(jié)果,又能對(duì)單個(gè)誤差因素的影響進(jìn)行仿真計(jì)算,便于精密測(cè)量?jī)x器及實(shí)驗(yàn)方法的精度分析與設(shè)計(jì)。
參考文獻(xiàn):
[1]IEEE Std 836-2001.IEEE recommended practice forprecision
centrifuge testing of linear accelerometers[S].
[2]BIPM/JCGM.Draft for discussion:Guide to the expres-sion of
uncertainty in measurement supplement 1.Nu-merical Method for the
Propagation of Distribution[M].2001.
[3]倪永勤.虛擬環(huán)境的間接測(cè)量不確定度評(píng)定與處理[J].微計(jì)算機(jī)信息,2007,23(4):103-105.
[4]趙宇,陳松濤,錢鍵.Monte-Carlo法在測(cè)量不確定度評(píng)定中的應(yīng)用[J].儀器儀表學(xué)報(bào),2004,25(4):501-504.
[5]王中宇.一種小樣本虛擬儀器不確定度評(píng)定新方法[J].計(jì)量學(xué)報(bào),2008,29(4):882-885.
[6]陳曉懷,薄曉靜,王宏濤.基于蒙特卡洛方法的測(cè)量不確定度的合成[J].儀器儀表學(xué)報(bào),2005,26(8):760-761.
[7]劉智敏.用MC仿真計(jì)算不確定度[J].中國(guó)計(jì)量學(xué)院學(xué)報(bào)[J].2005,16(1):2-4.
[8]CHRISTOS E P,HIO Y.Uncertainty estimation andMonte Carlo simulation method[J].Flow Measure-ment and Instrumentation.2001:291-298.
[9]崔孝海,曲璐.蒙特卡羅方法在微波功率測(cè)量不確定度分析中的應(yīng)用[J].計(jì)量學(xué)報(bào),2008,29(1):95-97.
[10]喬仁曉.線加速度計(jì)精密離心機(jī)法校準(zhǔn)建模與誤差補(bǔ)償[D].北京:北京航空航天大學(xué),2009:80-95.
[11]雷開彬,馬志霞.分段線性網(wǎng)格模型編輯技術(shù)[J].西南民族大學(xué)學(xué)報(bào),2008,34(3):577-583.
[12]陳全,鄧倩妮.云計(jì)算及其關(guān)鍵技術(shù)[J].計(jì)算機(jī)應(yīng)用,2009,(9):2-6.
[13]雷賢卿.圓度誤差的網(wǎng)格搜索算法[J].儀器儀表學(xué)報(bào),2008,29(11):2324-2329.
[14]陳康,鄭緯民.云計(jì)算:系統(tǒng)實(shí)例與研究現(xiàn)狀[J].軟件學(xué)報(bào).2009,20(5):1337-1348.
[15]許棟.微分網(wǎng)格處理技術(shù)[D].杭州:浙江大學(xué),2006:3-25.
標(biāo)簽:
相關(guān)技術(shù)
2、如涉及作品內(nèi)容、版權(quán)和其它問題,請(qǐng)?jiān)?0日內(nèi)與本網(wǎng)聯(lián)系,我們將在第一時(shí)間作出適當(dāng)處理!有關(guān)作品版權(quán)事宜請(qǐng)聯(lián)系:+86-571-88970062
- 金通靈風(fēng)機(jī)通過日本JFE鋼鐵株式會(huì)社驗(yàn)收
- 我國(guó)提出的全球首個(gè)電力儲(chǔ)能用 超級(jí)電容器國(guó)際標(biāo)準(zhǔn)成功立項(xiàng)
- 北京航天動(dòng)力研究所高性能安全閥保障全球最大綠色氫氨項(xiàng)目投產(chǎn)
- 聚焦現(xiàn)代化產(chǎn)業(yè)體系,江門市人大代表蒞臨凱特精機(jī)作專題調(diào)研
- “巨無霸”站起來了 中國(guó)石油自主技術(shù)模塊化聚丙烯環(huán)管反應(yīng)器成功吊裝
- 浙江三方控制閥召開海南商業(yè)航天發(fā)射場(chǎng)甲烷加注供氣系統(tǒng)低溫真空調(diào)節(jié)閥和低溫蝶閥出廠評(píng)審會(huì)
- 30家閥企中標(biāo)中國(guó)石化中壓球閥、美標(biāo)鑄鋼閥采購(gòu)項(xiàng)目
- 搶占西部化工升級(jí)紅利!2025成都國(guó)際化工裝備博覽會(huì)展位火速搶訂
- 青海最大跨流域調(diào)水工程歷經(jīng)29年建設(shè)全面投運(yùn)
- Wilo-Drainlift SANI家族污水提升系統(tǒng)再添新成員
- 東方自控"雙伺服閥油動(dòng)機(jī)"順利通過安全完整性等級(jí)(SIL2)認(rèn)證
- 中通協(xié)壓縮機(jī)分會(huì)團(tuán)體標(biāo)準(zhǔn)初稿討論會(huì)召開