分形樹狀通道換熱器內的流動換熱特性

                            陳永平,楊迎春,施明恒,吳嘉峰

                    (東南大學能源與環境學院,江蘇南京　210096)

        摘　要：建立了分形樹狀通道換熱器中層流流動與傳熱的三維穩態模型,采用流固耦合計算方法對入口水力直徑為4 mm的矩形截面樹狀通道內流動換熱進行了數值模擬,重點研究了分叉效應對傳熱的強化機理和換熱器受熱面的溫度分布。研究結果表明:分叉處形成的二次流能有效地強化換熱;與傳統的蛇形通道相比,分形樹狀通道換熱器具有溫度均勻性好、壓降小的明顯優勢。在相同入口雷諾數時,分形樹狀通道換熱器受熱面的最大溫差遠小于蛇形通道換熱器,另外,分形樹狀通道的層流流動壓降較之蛇形流道可減小50%以上。同時,加工了分形樹狀通道換熱器及蛇形通道換熱器各一套,對數值模擬結果進行了實驗驗證。實驗值與模擬值能較好地吻合,證明了所建流動換熱三維數值模型正確可信。

    關鍵詞：分形;換熱器;流動;傳熱;均溫性

    中圖分類號： V211·3; TK124　　　文獻標識碼：A

    文章編號：1000-6893(2010)03-0472-08

    可靠高效的熱控系統是保障航空飛行器安全飛行的首要前提之一,隨著航空飛行器制造技術的迅捷發展,其機載電子、電氣設備的熱可靠性指標也越來越苛刻,這就對機載換熱器件的換熱能力、泵功消耗以及溫度均勻性提出了更高的要求。因此,在航空熱控系統中,迫切需要研發結構優化的新型換熱設備以實現高效冷卻、散熱。

    仿生學經常能為設備優化提供有益啟示。比如,人體的呼吸循環系統是一個非常高效的傳熱傳質系統,人體中血管、氣管和淋巴管都是從宏觀尺度開始不斷分叉到細胞尺度,在這些分叉中,高層次和低層次的分叉結構都是相似的,該種結構被B.B.Mandelbrot[1]稱為分形結構。如將此分形結構應用于機載換熱器件的設計研發,應能大大提高其熱有效性,且由于通道呈樹網狀分布,可使換熱表面的溫度分布更加均衡。分形樹狀通道換熱器即是受此思想啟迪而發展起來的一種新型高效冷卻、散熱技術。

    近年來,在分形結構流動換熱研究領域已經取得了一定的進展,研究表明,分形結構對于提高系統的傳熱傳質效率具有很強的促進作用[2-13]。A.Bejan等[2]借鑒分形理論,提出了一套用于電子器件冷卻的樹狀結構換熱系統設計方案,并且指出該結構的泵功消耗與流動阻力較之平行結構大為減小。D.V.Pence等[3-5]在圓形散熱表面上設計了一套分形結構換熱器,但是考慮到常規的電子芯片大多為矩形表面,故該類圓形散熱器件的應用范圍相對比較狹窄。可是,單層矩形樹狀結構卻無法實現流體循環,針對這一問題,Y.P.Chen等[6]設計了一系列適用于矩形表面的三明治結構分形樹狀換熱器,使得分形結構更具實用性,研究發現,分形結構換熱器與傳統的平行通道換熱器相比具有更強的散熱能力和熱有效性。另外,為指導傳熱傳質系統的優化設計,A.Bejan等[14]又在分形理論的基礎上提出了一套用于系統優化設計的自構建理論。

    S.M.Senn等[15]對Y.P.Chen等[6]提出的分形樹狀結構中的層流流動換熱和壓降進行了數值模擬。X.Q.Wang等[16-17]分別對適用于圓形和矩形表面電子芯片散熱的分形樹狀換熱器進行了流動換熱研究,結果表明,分形通道壁面的溫度均勻性明顯優于平行通道。W.Wechsatol等[18]通過研究T型通道中的層流和湍流流動,提出在日趨微型化的電子芯片散熱中,不可忽視分叉效應對于強化換熱的關鍵作用。

    但是,由于受到分形結構復雜性和計算負荷較大的限制,現有的數值研究大多為一維或二維模型,即使少量的三維工作也并未很好考慮流固耦合。分形樹狀通道換熱器中傳熱傳質機理尚未得到全面揭示,尤其是分叉對流動和換熱的影響研究不夠全面,能夠更直觀地體現其優越均溫性的受熱面溫度分布研究也非常缺乏。為此,本文針對Y.P.Chen等[6]提出的三明治結構分形通道設計方案,建立了恒熱流條件下層流流動換熱的三維穩態模型,采用流固耦合計算方法對分形樹狀通道換熱器內流動換熱進行了數值模擬,重點研究了分形樹狀通道換熱器分叉處二次流的強化換熱作用及受熱表面的溫度分布特性,并與傳統蛇形通道進行了比較。同時,還加工了分形樹狀和蛇形通道換熱器各一套,對數值模擬結果進行了實驗驗證。

    1　分形網絡理論設計

    如圖1所示,參照人體呼吸系統的分形結構設計通道換熱器,分形分叉網絡生成方法如下:

    ①如圖1(a)所示,每一段通道在下一層次都有兩個分支,即N= 2,且Ф= 180°。

              

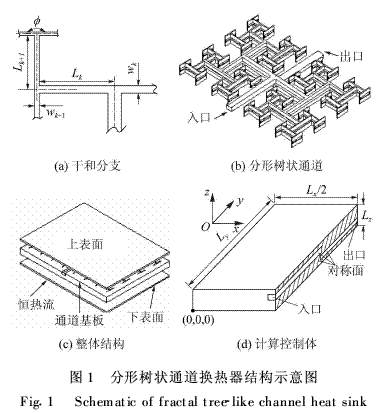
    ②k+1層次段的長度與k層次段長度的比值為

    

    式中:d0為初始通道水力直徑。現有研究表明[1],哺乳動物肺部支氣管分叉樹結構的指數Δ=3,鑒于肺中的空氣流動和傳熱過程相當有效,故選擇Δ=3作為水力直徑分形維數。通道分布如圖1(b)所示,通道級數為6,為了使冷卻流體能自由循環且散熱效果均勻,通道分為上、下兩層。下層通道除了出口與上層通道的進口方向相反外,其他都相同。各級通道均為矩形截面且深度h一致。上層通道中的最高級分叉末端皆有通孔與下層通道的分叉末端相連通。分形樹狀通道換熱器的整體結構見圖1(c),由上、中、下3塊鋁板制成,中間層通道基板上下表面上布置分形通道。如圖1(d)所示,換熱器關于x=Lx/2平面對稱,為了減少計算負荷,取整體的1/2為計算控制體。表1給出了分形樹狀通道的幾何參數。

               

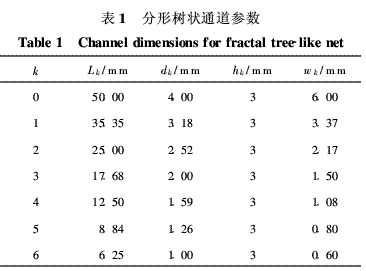
    另外,設計與分形樹狀通道換熱器具有相同受熱面積、通道換熱面積和入口幾何參數的蛇形通道,以比較兩者的溫度均勻性和壓降。蛇形通道如圖2所示。在圖1和圖2中的換熱器外型尺寸:Lx=138 mm,Ly=101·8 mm,Lz=16 mm。

              

    2　數學模型

    在計算控制體中(如圖1(d)所示),上表面和3個側面均為絕熱邊界條件,下表面為恒熱流邊界條件,其熱流密度q=2·5 W/cm2。根據換熱器的對稱性,定義x=Lx/2平面為對稱邊界條件。用去離子水作為冷卻介質,入口水溫為20℃,給定流體入口速度。在層流、常物性以及忽略體積力作用等假設的基礎上,建立三維穩態流動和傳熱耦合模型。

    2·1　控制方程
 

    

    2·2　邊界條件

    (1)流體的速度邊界條件

    在流固交界面上有流體無滑移邊界條件

               

              

    2·3　數值求解

    根據分形樹狀結構的對稱性,以x=Lx/2為對稱面,取0≤x≤Lx/2,0≤y≤Ly,0≤z≤Lz的部分作為計算控制體。由于分形通道呈網狀布置且各級通道尺寸存在較大差異,其結構較之傳統直通道遠為復雜;再者,考慮到流固耦合作用和分叉處附近出現的二次流,為保證計算精度,特對分形通道和固體部分均采用非結構網格,并在分叉處附近進行局部網格加密。另外,采用不同網格尺寸進行網格獨立性檢測,確保本文數值計算解均為網格獨立的解。為減小擴散誤差,采用二階迎風格式離散控制方程。

    基于控制容積有限差分法和求解壓力耦合方程的半隱式(Semi-implicit Method for PressureLinked Equation,SIMPLE)算法求解控制方程式(5)~式(8)。當流體速度殘差小于10-7,溫度殘差小于10-8,且進出口質量守恒和計算控制體能量守恒,即認為計算結果收斂。

    3　結果分析與討論

    3·1　流動特性

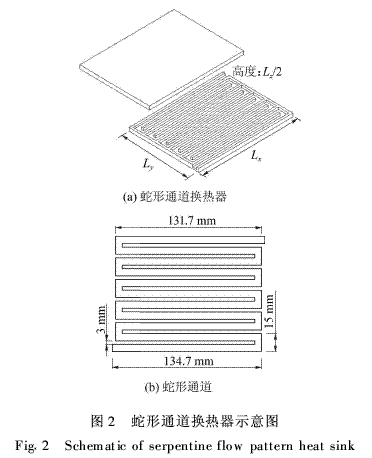
    分叉結構使得流體在通道中流經每一個分叉時均產生二次流,本文給出了一分叉處xOy截面和yOz截面的速度分布,截面位置如圖3所示,其對應的速度如圖4所示。

              

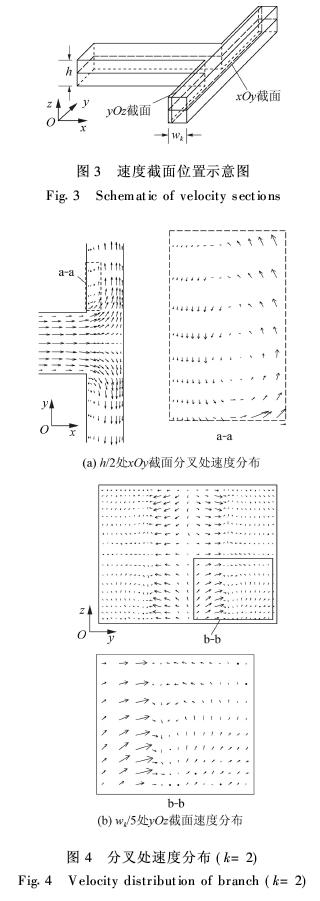
    圖4(a)為xOy截面分叉速度分布及分叉處二次流局部放大圖,在通道分叉處流體由沿x方向流動碰到壁面轉為沿y向流動,在內側壁面分叉點附近形成了二次流,即流體在分叉點附近產生回流和分離現象。圖4(b)分別為yOz截面速度分布及其1/4放大圖,可以看出,中間層流體與近壁面流體之間形成漩渦。這種二次流促進了流道中近壁面高溫流體與中間層低溫流體的相互混合,并伴隨流體射流沖刷壁面作用,從而強化了流動換熱。

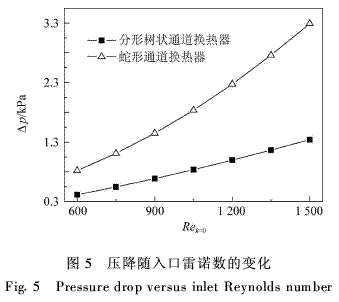
    需要指出的是,盡管在分形通道分叉處形成的二次流在強化換熱的同時也帶來了一定的壓降損耗,且隨循環層次的增加,通道尺度的減小將導致單位流量流體的單位長度壓降隨之增加,但是,更應注意到分形通道具有流體流量的分散作用,它實質上類似一流動的優化分散器,該結構可使各單元流體分散流動,流動距離較之具有相同流固換熱面積、集中流動的蛇形結構中流動距離大為減小,比如,本文中分形結構的流體流動距離(上下兩層)為311·24 mm,而蛇形通道中流體的流動距離為1 202·5 mm,前者僅為后者的25·9%。流動長度的大比例縮短不僅有效地抵消了分叉及尺度縮小所導致的壓損增加,且使得分形結構在總體上與蛇形通道相比具有壓降小的明顯優勢。圖5給出了兩種通道換熱器的壓降Δp隨入口雷諾數Rek=0的變化情況。在相同入口雷諾數時,流體層流流動壓降僅為蛇形流道中的一半,與S.M.Senn等[16]的結論基本一致。

             

    3·2　溫度分布

    圖6給出了相同入口雷諾數時,分形樹狀通道和蛇形通道受熱面的溫度分布。兩種通道的換熱器具有相同入口幾何參數、相同通道換熱面積、相同受熱面積以及相同外型尺寸。從圖6可以看出兩種通道換熱器的受熱面溫度分布有較大的差別。在分形網絡結構中,各級通道之間的換熱是相互關聯的,其中最為明顯的是0級通道與其相鄰的末級通道之間的相互影響,因此,最低溫度出現在如圖6(a)所示的換熱器中心位置,并從該位置向外周溫度逐漸升高,但總體溫差不大。而蛇形換熱器通道之間的換熱影響較小,入口側與出口側溫差較大。顯然,前者在溫度均勻性方面具有突出的優勢。


    在本文中,均溫性以恒熱流條件下受熱面上出現的最高溫度tb,max和最低溫度tb,min之差加以表征。定義受熱面的最大溫差為Δtmax= tb,max-tb,min(18)

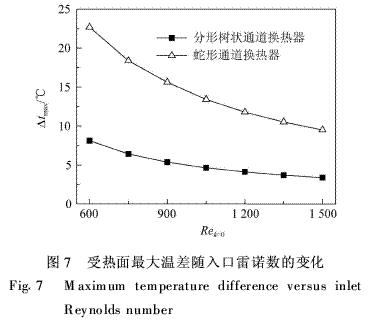
    相同熱流條件下,Δtmax越小,其均溫性越強。圖7給出了具有相同入口幾何參數、相同通道換熱面積、相同受熱面積以及相同外型尺寸的分形樹狀通道換熱器和蛇形通道換熱器均溫性的比較。由圖可知,隨著入口雷諾數的增加,兩種換熱器的最大溫差均逐漸減小且變化趨勢逐漸平緩,但是分形樹狀通道換熱器的最大溫差遠小于蛇形通道換熱器。再一次驗證了分形樹狀換熱通道具備優越的均溫性。
 

    4　實驗驗證

    4·1　實驗裝置

    為驗證所建層流流動換熱三維模型的正確性,分別加工了一套與數值模擬所用結構尺寸相同的分形樹狀通道換熱器和蛇形通道換熱器,測量了兩套換熱器的受熱面溫度分布及進出口壓力差。實驗測試系統如圖8所示。

                 

    分形樹狀通道換熱器的上、下蓋板和通道基板用螺栓和Ο型墊圈密封連接,電加熱塊和換熱器之間用螺栓固定,接觸面之間涂導熱膠以減少接觸熱阻。整個實驗段外包保溫材料減少散熱損失。蛇形通道換熱器的安裝也與之類似。實驗中,采用電加熱塊提供恒熱流,通過改變加熱功率實現換熱工況調節,輸入功率由功率表測得。冷卻介質為恒溫水浴提供的20°C去離子水,通過調節閥門的開度以提供不同的冷卻條件。采用玻璃轉子流量計測量流量,用數字差壓傳感器測量進出口壓力差。熱電偶信號和差壓傳感器信號均由Agilent 34970A數據采集儀采集。

    4·2實驗結果

    根據數值模擬中分形樹狀通道換熱器和蛇形通道換熱器受熱面溫度分布特點在受熱面上布置具有代表性的測溫點,并按照溫度從低到高的順序對測溫點進行編號,如圖9所示。
 

               

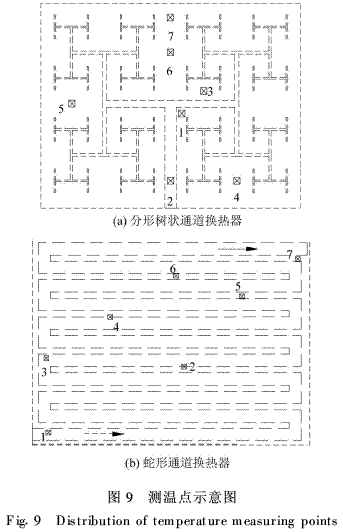
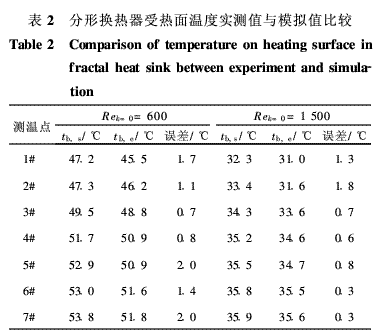
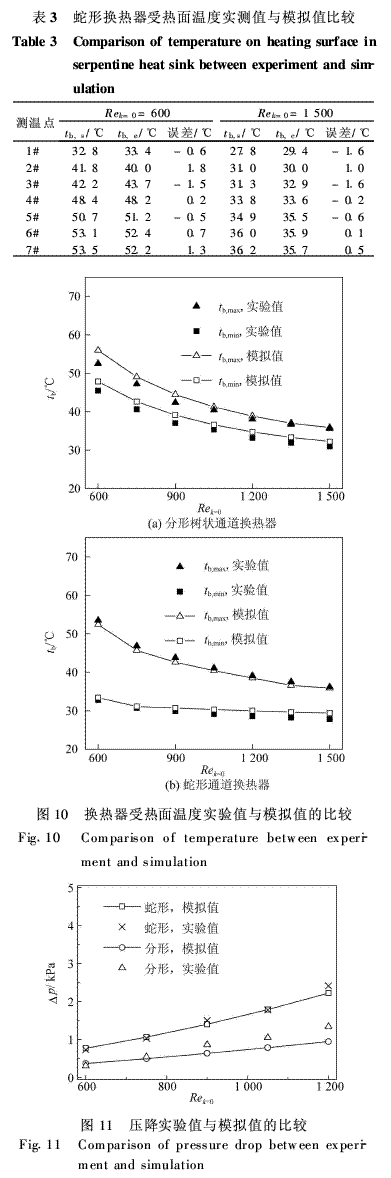
    表2和表3分別列出了分形樹狀通道換熱器和蛇形通道換熱器在入口雷諾數分別為600和1 500時,7個測溫點處的溫度實測值和模擬值。可以看出,兩表中實測數據皆從1#到7#依次升高,與模擬值的變化趨勢一致。圖10給出了兩套換熱器在不同入口雷諾數時受熱面上實測最高、最低溫度tb,e與模擬最高、最低溫度tb,s的比較。從表2、表3和圖10均可以看出,兩套換熱器溫度實驗數據與模擬值皆吻合較好。圖11給出了不同入口雷諾數時,分形樹狀通道換熱器和蛇形通道換熱器沿程壓降實驗測量值與模擬值的比較,可以看出,壓降的實驗數據與模擬值同樣基本吻合。這就證明本文所建立的流動換熱三維模型準確可靠。

            

    5　結　論

    (1)在分形樹狀通道內,流體流經每一個分叉時在分叉點附近形成二次流,即產生回流和分離現象。這種二次流促進了流道中近壁層的高溫流體與中心處的低溫流體間的相互混合,并伴隨流體射流沖刷壁面作用,從而強化了流動換熱。

    (2)與傳統的蛇形通道相比,分形樹狀通道換熱器具有溫度均勻性好、壓降小的明顯優勢,在航空熱控系統中有著廣闊的應用前景。在相同入口雷諾數時,分形樹狀通道換熱器受熱面的最大溫差Δtmax遠小于蛇形通道換熱器,且隨著入口雷諾數的增加,Δtmax逐漸減小。另外,分形樹狀通道的層流流動壓降較之蛇形流道可減小50%以上。

    (3)本文壓降和溫度的模擬值與實驗測量值均能較好地吻合,這證明本文所建三維穩態模型準確可信。

    參考文獻:略